maxValue = maximize . fmap static . prune 5 . gameTreeEpisode Three: Higher-order functions and data type evolution
In episode one we made the case for incremental development and the importance of staying non-intrusive. What we will do now is changing code from the last increment.
A stack of increments
Changing code is what we declared as being intrusive but changing the last increment is allowed.
The problem with changing code is that any code that depends on it may be compromised. That is the intrusion. Since no code can possibly depend on the last increment, changing it is safe.
With that consideration out of the way, let’s look at our last increment that finds the minimax value for a given board:
It works fine but we would like to make it even more idiomatic in the functional sense.
We have already seen that functional programmers like to introduce abstractions very early and there is a hidden abstraction in the code above as we might want to find the maxValue for different versions of static evaluation.
Our given static function happens to be just one of possibly many functions that we might want to use for evaluation while the minimax evaluation approach is the same for all evaluations.
So, let’s separate the two: make a general evaluateBy function that can be parameterized with a specific function that evaluates a single board.
Generalizing static into fmap static
evaluateBy f = maximize . fmap f . prune 5 . gameTree
maxValue = evaluateBy staticNote that evaluateBy now takes a parameter f, which can be any function that takes a Board and returns an Ord as required by maximize.
A function like evaluateBy that takes another function as a parameter is called a higher-order function. They are heavily used in functional programming and in fact we have used them before without giving it any attention. The current case, though, is different. We use this very common functional feature to set the stage for non-intrusive increments.
A new requirement comes up: predicting the future
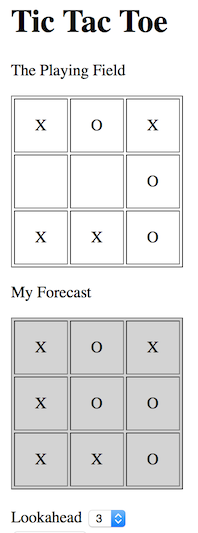
It appears that playing the game is fun but sometimes it is difficult to understand why the computer does a certain move. It would be interesting if we had a some insight and could show what the computer is considering. The idea is that we display a forecast: the final board that the computer thinks the game will develop into.
Computer knows he will win.
To this end, we need to capture the board that led to the minimax value. It turns out that this is easier than expected. We can use evaluateBy but we do not pass the static function any more. Instead, we pass a function that maps a board not only to its static value but to a pair of the static value and the board itself.
Pairing up the static value with its board
endValue = evaluateBy capture where
capture board = (static board, board)This is nice. First and foremost it is a fully non-intrusive increment! We did not change any existing code at all.
Second, it falls in place very naturally when following the functional style with higher-order functions - without any anticipation of new requirements.
The downside is: it doesn’t compile.
Our mapping function must return an Ord but a pair (any tuple actually) is only of type Ord if all its elements are of type Ord as well. The Double value is but the Board type is not.
Hm, what next? Going back to the definition of Board and changing its definition? That would be an intrusive change.
Here we see a big benefit of Frege typeclasses (as opposed to let’s say Java interfaces): we can evolve the data type! Board becomes an instance of the Ord typeclass non-intrusively in a new increment with full static type safety!
There is not much logic to add since we make all boards equal. For the purpose of ordering our pairs we only need the static Double values of the pair.
All Boards are created equal…
instance Ord Board where (<=>) a b = EQThis code looks so simple but the implications are huge. By making Board an instance of Ord, we have given the Board type a new capability!
Now we have everything compiling and working. You can play the game and see the forecast working.
In the next episode, we will apply a rather unconventional increment: going safely parallel.